التفاضل والتكامل فرع من فروع الرّياضيات التي تستكشف المتغيرات وكيفية تغيّرها عبر النظر إليها بقيم صغيرة تدعى «الكمية المتناهية في الصغر- infinitesimals.»
وكان العالِم البريطانيّ اسحق نيوتن (1642 – 1726) والعالِم الألمانيّ جوتفريد لايبنتس (1646 – 1716)، تمكنا من ابتكار التفاضل والتكامل القرن السابع عشر كما ندرسه اليوم، فطوّر كل منهما بشكل مستقل المبادئ الأساسيّة للتفاضل والتكامل، لكن الأول اعتمد على علم الهندسة، بينما انطلق الثاني من علم «الرياضيات الرمزية – Symbolic Mathematics.»
 

ما الفائدة من الكميات المتناهية في الصغر؟
من أجل فهم ماذا تعني الكميات المتناهية في الصغر، لنأخذ الصيغة الرياضية المعبرة عن مساحة الدائرة؛ أي العلاقة التالية: A=πr²، والتي أشار الأستاذ ستيف ستروجاتس من جامعة كورنيل أنه على الرغم من بساطتها إلّا أنه من المستحيل اشتقاقها من دون وجود القيم المتناهية في الصغر.
بداية وجدنا أن النسبة بين محيط الدائرة وقطرها تساوي قيمة ثابتة تبلغ تقريباً 3.14، وهي النسبة التي نسميها pi وتكتب بالشكل (π)، وباستخدام هذه المعلومات نكتب أيضاً صيغة محيط الدائرة بالشكل: C=2πr؛ (r هو نصف القطر). ولحساب مساحة الدائرة تبدأ بتقطيع الدائرة إلى ثمانية أقسام وإعادة ترتيبها لتصبح بالشكل التالي:

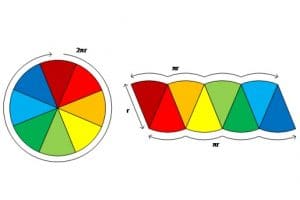
ونلاحظ أن الضلع القصير المستقيم يعادل نصف قطر الدائرة الأساسيّ (r)، بينما يعادل الجانب الطويل المنحني نصف محيط الدائرة(πr). وإذا كررنا ذلك باستخدام 16 جزءاً، سيبدو على الشكل كالتّالي:

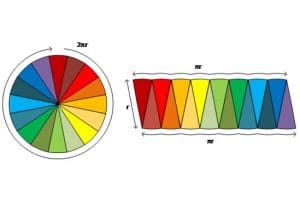
ونرى مجدداً أن الضلع القصير المستقيم يعادل نصف قطر الدائرة الأساسيّ (r)، والجانب الطويل المتعرج يعادل نصف محيط الدائرة(πr)، لكن الزاوية المحصورة بين الجوانب قريبة للزاوية القائمة والجزء الطويل أقل تعرجاً. ومهما زدنا عدد الأجزاء التي نقطع الدائرة بها، سيحافظ الضلع القصير والجانب الطويل على الطول المحدد لكل منهما، وستقترب الزاوية بين الجوانب تدريجياً من الزاوية القائمة، ويصبح الجانب الطويل أقل تعرٌّجاً.
لنفترض الآن أنّنا قطّعنا العدد 3.14 لأعداد لا متناهية من الشرائح. حيث نجد في لغة الرياضيات، أن الشريحة توصف «كسماكة متناهية في الصغر» لكن عندما يتناهى عدد الشرائح إلى اللانهاية تبقى الأضلاع تساوي الطول r و3.14*r، لكن الزّاوية بين جميع الجوانب تصبح زاوية قائمة ويصبح التعرج في الجانب الطويل معدوماًـ ويعني هذا أنه أصبح لدينا شكل مستطيل.

حساب مساحة المستطيل هذا هو كما تعرفون يساوي الطول*العرض: πr × r= πr²، وهذا مثال يوضّح قوة دراسة متغير، مثل مساحة الدائرة كمجموعة من الكميات المتناهية في الصغر.

نصفيّ التكامل والتفاضل
تتكون دراسة التكامل والتفاضل من جانبين. يدعى الأول، «التفاضل _ differential calculus» وهو يركّز على الدراسة الفردية للكميات المتناهية في الصغر، وماذا يحدث في الأجزاء اللامتناهية بالصغر. أمّا الجانب الثاني من التفاضل والتكامل، فيدعى «التكامل _ integral calculus» حيث يعتمد على إضافة عدد لانهائي من الكميات المتناهية في الصغر معاً (كما في المثال السابق). وهما عمليتان متعاكستان ويشار إليهما بأنهما عموماً النظرية الأساسية في علم التكامل والتفاضل. ولكي نكتشف كيف تعمل هذه النظرية، لنأخذ المثال التالي من حياتنا اليومية:
لدينا كرة رميناها نحو الأعلى باتجاه عمودي من ارتفاع ابتدائي يبلغ ثلاثة أقدام (0.9144 متر) بسرعة أوليّة قيمتها 19.6 قدم/ثانية. فإذا رسمنا بيانياً موقع تغيّر الكرة خلال الزمن، نحصل على شكل مألوف يدعى بالقطع المكافئ.

التفاضل
تغيّر الكرة سرعتها في كل نقطة على طول المنحني ولا يوجد زمن تحافظ فيه الكرة على معدّل سرعة ثابت، لكننا نستطيع حساب متوسط السرعة في أي مدة زمنية. فمثلاً، لإيجاد معدّل السرعة من 0.1 ثانية إلى 0.4 ثانية، نجد الموقع للكرة بين هذين الزمنين ونرسم خطاً بينهما. ونلاحظ هذا الخط يرتفع مع ازدياد عرضه. وتسمى هذه النسبة غالباً الميل، وتعرف بأنها حاصل قسمة الارتفاع على العرض. وعلى الرسم البياني الزمني، يمثّل المنحدر السرعة، ويرتفع الخط من 4.8 قدم إلى 8.3 قدم أي حوالي 3.5 قدم. ويتغير الزمن من 0.1 ثانية إلى 0.4 ثانية أي أن المدة هي 0.3 ثانية. ميل هذا المستقيم هو معدّل سرعة الكرة خلال هذه المدة، ويساوي حاصل قسمة الارتفاع على تغير الزمن أي 3.5 قدم تقسيم 0.3 ثانية = 11.7 قدم في الثانية

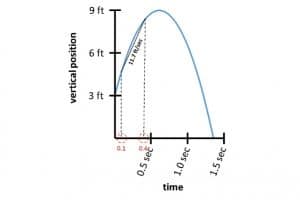
في اللحظة 0.1 ثانية، نرى أن التقوس في الخط البياني حاد قليلاً مقارنة بالمتوسط الذي حسبناه، وهذا يعني أنّ الكرة كانت تتحرك بسرعة أسرع قليلاً من 11.7 قدم/ثانية، أما في اللحظة 0.4 ثانية فإن التقوس للخط البياني أعلى بقليل من المستوى، و هذا يدلّ أن الكرة كانت تتحرك بسرعة أقل من 11.7 قدم/ثانية. ولأن السرعة كانت تتناقص فهذا يعني أنه يجب أن يكون لدينا لحظة معينة كانت تتحرك فيه الكرة بسرعة 11.7 قدم/ثانية تماماً، فكيف نحدد الزمن الدقيق لهذه اللحظة؟
لنعود إلى الوراء ونلاحظ أن المدى الزمني بين 0.1 ثانية و0.4 ثانية ليس الزمن الوحيد الذي تكون فيه للكرة معدّل سرعةً يبلغ 11.7 قدم/ثانية. لذا إذا حافظنا على الميل نستطيع أن ننقله إلى أي مكان على المنحني ونحصل على معدّل السرعة ذاته الذي يساوي 11.7 قدم/ثانية في المدى الزمني بين النقطتين التي يتقاطع فيهما مع المنحني. إذا نقلنا المستقيم أكثر باتجاه ذروة القطع المكافئ، فإن المدى الزمني يتناقص. عندما يصل الزمن إلى الصفر، فإن نقطتي التقاطع تقع في المكان ذاته ويصبح المستقيم ملامساً للقطع (بالكاد يمسّه)، ويوصف المدى الزمني بأنّه متناهي إلى الصفر.
تدخل هنا فكرة الكمية المتناهية في الصغر حيّز التنفيذ، فبعد أن تكلمنا عن السرعة خلال مدّة معينة من الزمن، نتحدث عن السرعة خلال لحظة؛ أي مدّة زمنية متناهية الصغر. لاحظ كيف أننا لا نستطيع أن نأخذ المنحني بين نقطتين متناهيتي الصغر في البعد؛ سوف يكون لدينا حاصل قسمة الارتفاع على الزمن أي صفر على صفر وهذا ليس له معنى. لإيجاد الميل في أيّ نقطة على الخط البياني، نجد الميل للمستقيم الملامس (المماس)، والنتيجة النقاط الستة المرسومة هنا:

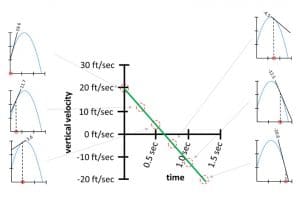
ميل المماس لستة نقاط للحصول على المشتقات (صورة)
يعرف هذا الرسم البياني بالرسم البياني الأصلي للمشتق. وفي لغة الرياضيات والفيزياء، نقول «مشتق المكان بالنسبة للزمن هو السرعة.»

التكامل
هي العملية المعاكسة للتفاضل، فتكامل السرعة لجسم معين بالنسبة للزمن هو مكان وجوده. ويحسب الاشتقاق كما وجدنا عن طريق إيجاد المنحنيات؛ بينما يحسب التكامل عن طريق إيجاد قيم المساحات.
تقابل السرعة الزمن على الرسم البياني، وتمثل المساحة المسافة، وإيجاد المساحات على الرسم البياني أمر بسيط نسبياً عند التعامل مع المثلثات والمعينات، لكن عندما نتعامل مع رسم بياني متعرّج بدلاً من الخطوط المستقيمة، يصبح من الضروري تقسيم المساحة إلى عدد لانهائي من المثلثات الصغيرة (هذا مشابه لجمع عدد لانهائي من الأجزاء المتناهية في الصغر من أجل حساب مساحة الدائرة).

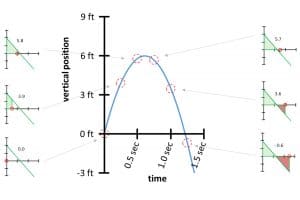
يعطي مجموع المنطقة تحت ست نقاط من تابع التكامل، والمساحات تحت المحور س (بالأحمر) سالبة، لذلك تنقص من المساحة الكلية. (صورة)
ربما لاحظت أن الرسم البياني للتكامل لا يعطينا تماماً الرسم البياني للموقع العمودي الذي بدأنا منه، لأنه واحد من عدة رسوم بيانية للمواقع العمودية التي جميعاً المشتق ذاته، وتظهر عدّة منحنيات متشابهة هنا:

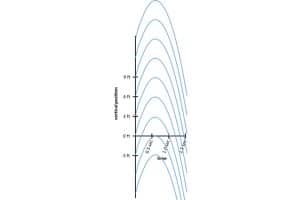
بعض الأمثلة لمنحنيات المكان التي تملك جميعاً المشتق ذاته. يُميّز المنحني المطلوب عن طريق الشرط الابتدائي، الذي يظهر كدائرة حمراء منقّطة.(صورة)
من أجل أن نحدد أياً من هذه المنحنيات ستعطينا الموقع الأصليّ للرسم البياني، يجب أن نعرف مكان الكرة في زمن معين.
من الأمثلة على ذلك الارتفاع الذي رميت منه الكرة (ارتفاع الكرة في لحظة الزمن صفر)، أو اللحظة التي اصطدمت فيها الكرة بالأرض (الزمن عندما كان الارتفاع يساوي الصفر). يشير هذا إلى الشرط الابتدائي، لأننا عادةً نجري حسابات لتوقع القيم بعد هذا الشرط، وقد تظن أنه يوجد خطأ في تسميته، لأن هذا الشرط الابتدائي قد يأتي في منتصف أو نهاية الرسم البياني.
 

المصدر : أنا أًصدق العلم